Parallelizing numerical simulations requires efficient data exchange between processes, particularly for stencil-based computations like 2D wave propagation. In this project, I implemented ghost cell communication using MPI, allowing each process to exchange boundary data with its neighbors while minimizing synchronization overhead.

Optimization Strategy

To enhance performance, I employed multiple MPI-based optimizations:

1. Domain Decomposition and Ghost Cells
   • The global grid was divided among processes into sub-grids, each with an additional ghost cell layer to facilitate communication.
   • Implemented absorbing boundary conditions at the global edges.
2. Efficient MPI Communication
   • Initially used blocking MPI_Send and MPI_Recv, which was later replaced with non-blocking MPI_Isend and MPI_Irecv to overlap computation with communication.
   • Optimized MPI calls by splitting communication into east/west exchanges followed by north/south exchanges, reducing the total send/receive pairs from 8 to 4.
3. Custom MPI Datatypes for Efficient Data Transfer
   • Used MPI_Type_vector for column exchanges and MPI_Type_contiguous for row exchanges, optimizing memory layout and minimizing redundant memory copies.
   • Applied MPI_Waitall to reduce synchronization overhead.
4. Cache-Aware Memory Layout
   • Optimized row-major traversal to improve cache efficiency, reducing memory access latency.

Performance Analysis

I evaluated the scalability of the implementation across different core counts:

1. Strong Scaling Study
   • Achieved near linear scaling up to 128 cores, with efficiency dropping beyond that due to communication overhead.
   • At 16 cores, performance reached 5.04 GFLOPS, scaling up to 90.72 GFLOPS at 384 cores.
2. Weak Scaling Study
   • Observed a steady increase in runtime, indicating that communication costs outpaced computational gains as core counts increased.
   • Confirmed that the implementation did not exhibit ideal weak scaling, likely due to increasing ghost cell communication overhead at larger process counts.
3. Impact of Grid Geometry on Performance
   • Balanced processor geometries (square-like partitions) resulted in higher performance, minimizing communication bottlenecks.
   • Highly skewed partitions (e.g., 1x128 instead of 32x4) increased communication overhead, reducing overall efficiency.

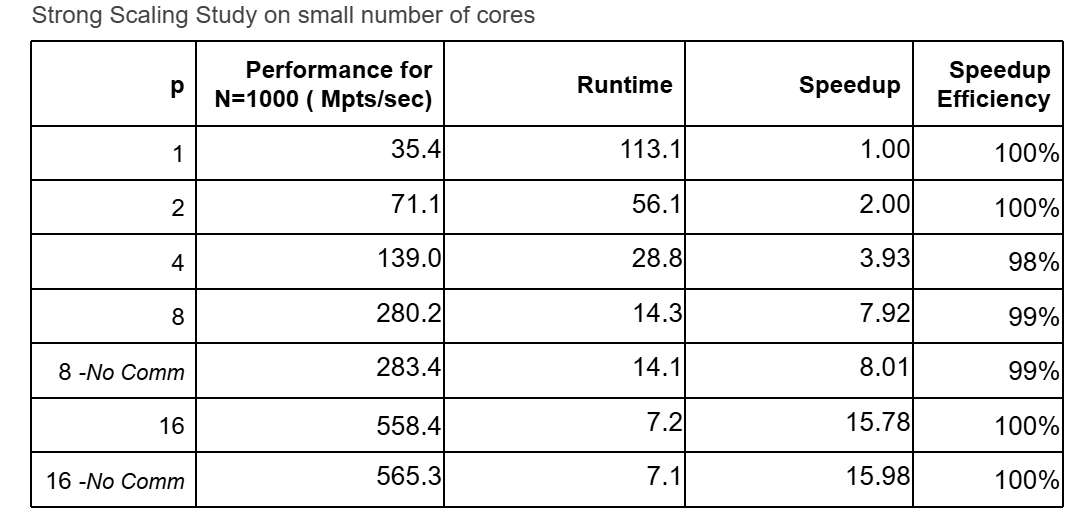This table shows how increasing the number of cores improves performance. With 16 cores, the speedup reaches 15.78x, demonstrating efficient parallelization. The No Comm rows indicate minimal overhead from communication, showing that inter-process exchanges are well-optimized.

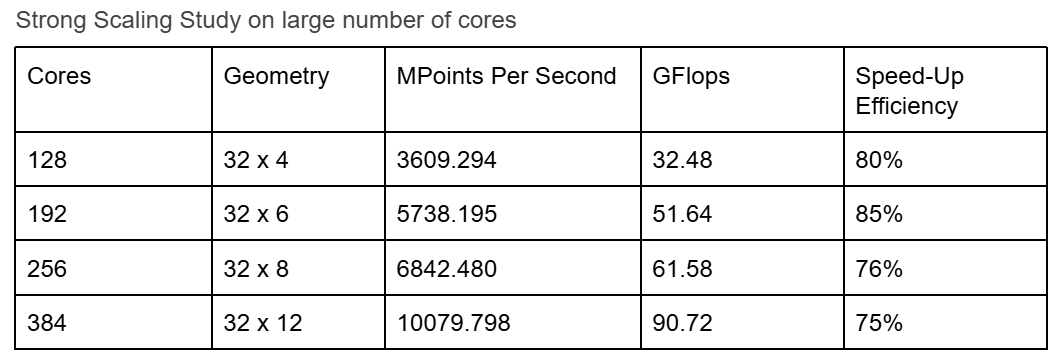Performance scales up to 384 cores, achieving over 10,000 million points per second (MPts/sec) and 90.72 GFLOPS. However, speedup efficiency drops slightly as communication overhead becomes more significant at extreme core counts.

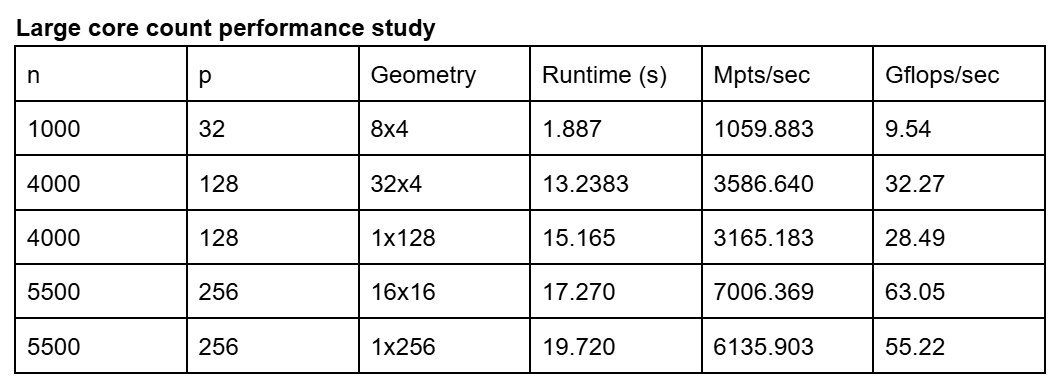This study compares different processor geometries, highlighting how balanced core layouts (e.g., 32x4 or 16x16) perform better than highly skewed ones (e.g., 1x128 or 1x256). The best performance is achieved with a 16x16 configuration, reaching 63.05 GFLOPS.

This project provided hands-on experience in MPI programming, domain decomposition, and optimizing inter-process communication, reinforcing my understanding of scalable parallel computing techniques.

« GPU Matrix Multiplication Optimization Reducing Token Usage with GPT-2 »