Matrix multiplication is a fundamental operation in high-performance computing, and optimizing it for GPUs requires an in-depth understanding of memory hierarchy, parallel execution, and warp scheduling. In this project, I implemented a highly optimized CUDA-based matrix multiplication kernel, leveraging 2D tiling, shared memory, and interleaved computation to maximize efficiency.

Optimization Strategy

The optimized implementation followed a multi-layered approach to maximize GPU throughput:

1. 2D Tiling with Shared Memory
   • Implemented 2D tiling where each thread block processes a tile of matrix C.
   • Used shared memory to store tiles of matrices A and B, reducing global memory accesses and improving memory bandwidth utilization.
2. Thread Workload Scaling (TILESCALE_M and TILESCALE_N)
   • Instead of each thread computing a single element of matrix C, threads computed multiple elements, maximizing register reuse and minimizing memory latency.
   • Experimented with different TILESCALE values, achieving optimal performance with TILESCALE_M = 4, TILESCALE_N = 4, reaching ~3.7 TFLOPs for N = 2048.
3. Thread Block and Tile Size Tuning
   • Experimented with multiple thread block sizes (64, 256, 1024) and identified that 256 threads was optimal for N = 256 and N = 512, balancing parallelism and resource utilization. 1024 threads provided the best performance for larger matrices (N ≥ 1024) by maximizing warp execution efficiency.
4. Edge Case Handling
   • Implemented zero-padding and boundary checks for non-multiples of the tile size.
   • Observed performance drops at non-multiples of 128 due to suboptimal memory access patterns and cache inefficiencies.

Performance Analysis

I compared three implementations:

1. Naïve Matrix Multiplication – Each thread computed a single element of matrix C, leading to excessive global memory accesses and poor performance.

2. Optimized 2D Tiling Implementation – Introduced shared memory, warp-level optimizations, and tile-based computation, significantly reducing memory bottlenecks.

3. Final Optimized Kernel with Interleaved Computation – Implemented TILESCALE-based workload distribution, maximizing register utilization and achieving ~3.7 TFLOPs at N = 2048.

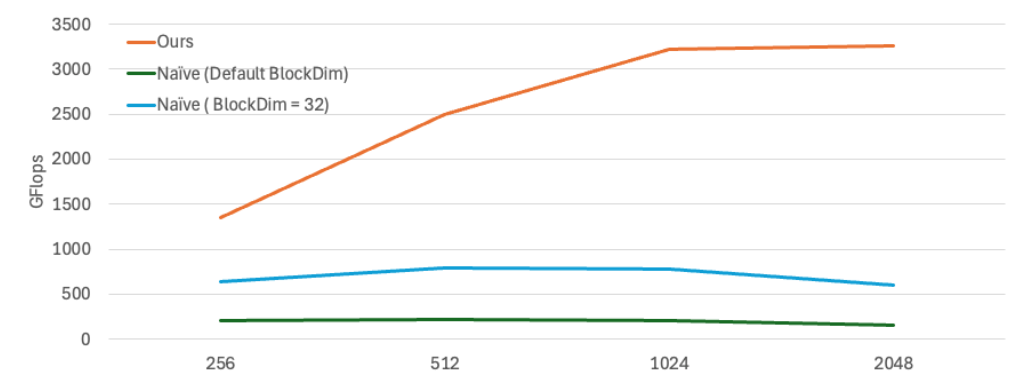
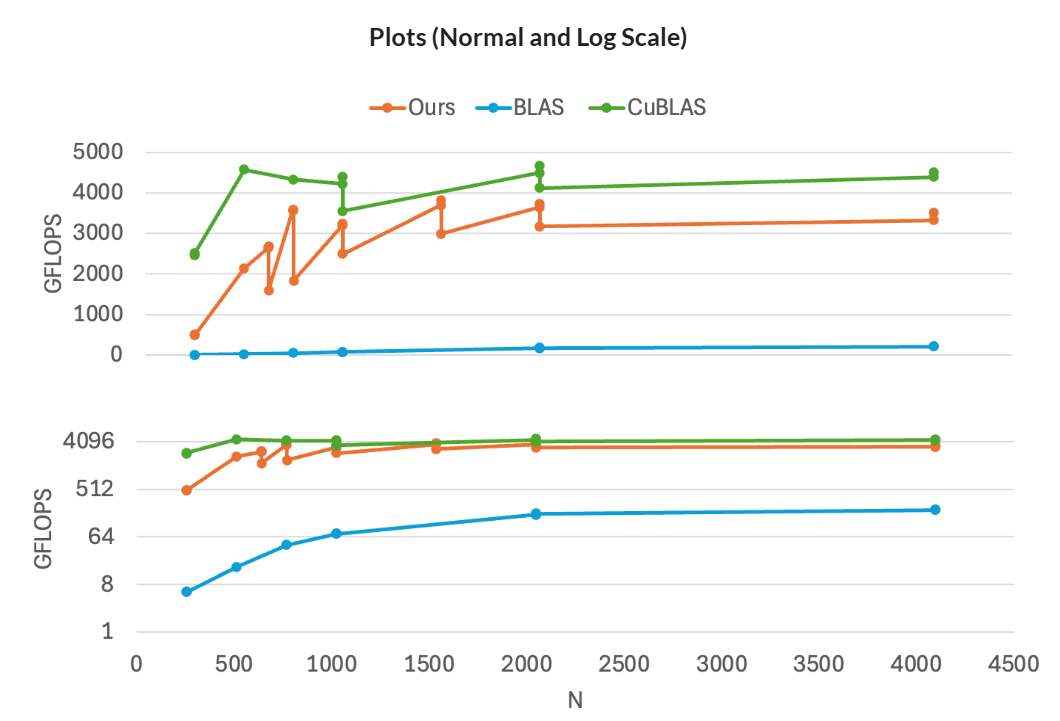These plots compare the performance of my optimized GPU matrix multiplication against standard libraries and naïve implementations. The first plot shows how my implementation outperforms BLAS and comes close to cuBLAS at larger matrix sizes. The second plot compares my optimized kernel with naïve approaches, demonstrating how block size tuning and shared memory optimizations significantly improve GFLOPS performance, whereas naïve implementations plateau early. These results showcase the impact of efficient memory access and parallelization in high-performance GPU computing.

This project provided hands-on experience in CUDA kernel optimization, memory hierarchy tuning, and warp-level parallelism, reinforcing my understanding of high-performance GPU computing.

« Building a GPT Model from Scratch Ghost Cell Exchange in Parallel Computing »