Matrix multiplication is a critical operation in high-performance computing, and optimizing it requires an in-depth understanding of memory hierarchy, vectorization, and instruction-level parallelism. In this project, I implemented an optimized DGEMM (Double-precision General Matrix Multiplication) routine that achieved significant performance improvements using ARM Scalable Vector Extension (SVE) intrinsics, hierarchical blocking, and memory packing.

Optimization Strategy

The optimized implementation followed a four-layered approach to maximize performance:

1. Memory Packing for Cache Efficiency
   • Implemented row-major and column-major packing for matrices A and B to improve spatial and temporal locality.
   • This reordering allowed for sequential memory access, reducing cache misses and improving bandwidth utilization.
2. Cache-Optimized Blocking
   • Broke down matrices into cache-friendly blocks to ensure efficient use of L1, L2, and L3 caches.
   • Selected optimal blocking parameters (MC = KC = NC = 256; MR = 64; NR = 4) through experimentation.
3. Macro-Kernel for Vectorized Execution
   • Designed a macro-kernel optimized for ARM SVE’s vector length (VLEN) to maximize instruction throughput.
   • Applied loop unrolling and register blocking to improve instruction-level parallelism (ILP).
4. SVE Micro-Kernel with SIMD Acceleration
   • Developed a 16x4 SVE micro-kernel that leveraged ARM SVE intrinsics for vectorized computations.
   • Used fused multiply-add (FMA) operations to speed up accumulation in matrix C.
   • Processed multiple elements in parallel, leading to a high-performance gain of ~18-20 GFLOPs.

Performance Analysis

I compared three implementations:

1. Naïve Matrix Multiplication – Basic triple loop implementation with inefficient memory access patterns.

2. OpenBLAS Implementation – Highly optimized industry-standard matrix multiplication.

3. My Optimized Implementation – Achieved near-OpenBLAS performance using SVE intrinsics, loop unrolling, and hierarchical memory optimizations.

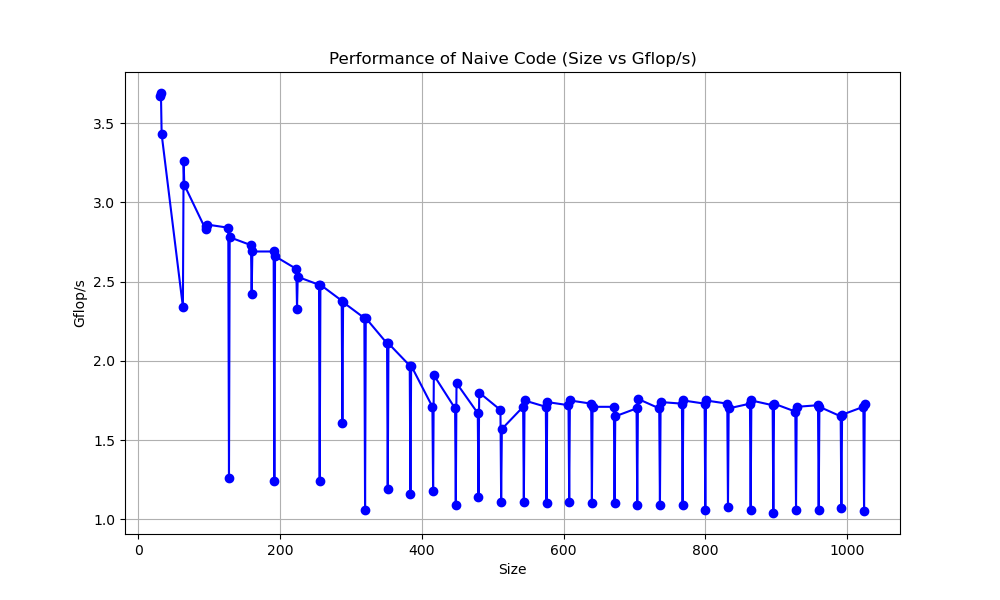
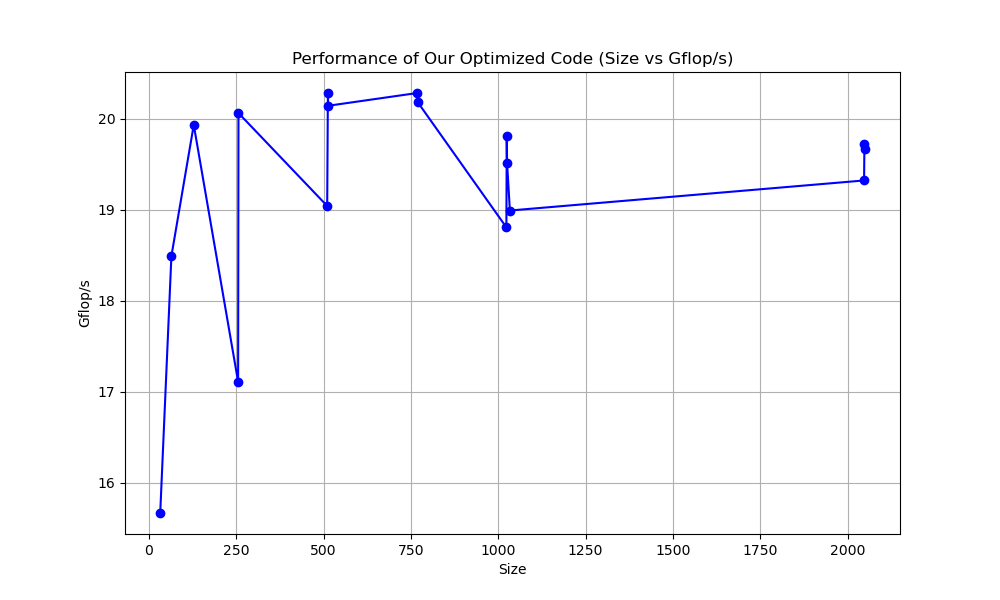
Despite initial challenges with loop unrolling and vector register allocation, I successfully optimized the micro-kernel to process multiple rows of matrix C in parallel while minimizing overhead. The final implementation demonstrated significant speedup compared to the naïve approach, particularly for larger matrices where cache and vectorization benefits were maximized. The speedup using my code was almost ten times faster than the naive code. This project deepened my understanding of parallel computing, memory hierarchy, and SIMD optimizations, providing practical experience in high-performance computing (HPC) and ARM architecture optimizations.

« Seamgen - Statewide Vulnerability Assessment (SVA) Project Building a GPT Model from Scratch »